Categorical Deep Q-Networks

Objective

The main objective of Categorical Deep Q-Networks is to learn the distribution of Q-values as unlike to other variants of Deep Q-Networks where the goal is is to approximate the expectations of the Q-values as closely as possible. In complicated environments, the Q-values can be stochastic and in that case, simply learning the expectation of Q-values will not be able to capture all the information needed (for eg. variance of the distribution) to make an optimal decision.

Distributional Bellman

The bellman equation can be adapted to this form as

\[Z(x, a) \stackrel{D}{=} R(x, a) + \gamma Z(x', a')\]

where \(Z(s, a)\) (the value distribution) and \(R(s, a)\) (the reward distribution) are now probability distributions. The equality or similarity of two distributions can be effectivelyevaluated using the Kullback-Leibler(KL) - divergence or the cross-entropy loss.

\[Q^{\pi}(x, a) := \mathbb{E} Z^{\pi}(x, a) = \mathbb{E}\left[\sum_{t=0}^{\inf} \gamma^{t} R(x_t, a_t)\right]\]

z sim P(odot vert x_{t-1}, a_{t-1}). a_t sim pi(odot vert x_t), x_0 = x, a_0 =a

The transition operator \(P^\pi : \mathcal{Z} \rightarrow \mathcal{Z}\) and the bellman operator \(\mathcal{T} : \mathcal{Z} \rightarrow \mathcal{Z}\) can be defined as

\[P^{\pi}Z(x, a) \stackrel{D}{:=} Z(X', A') ; X' \sim P(\odot \vert x, a), A' \sim \pi(\odot \vert X')\]

\[\mathcal{T}^{\pi}Z(x, a) \stackrel{D}{:=} R(x, a)+ \gamma P^{\pi}Z(x, a)\]

Algorithm Details

Parametric Distribution

Categorical DQN uses a discrete distribution parameterized by a set of supports/atoms (discrete values) to model the value distribution. This set of atoms is determined as

\[{\mathcal{z}_i = V_{MIN} + i \nabla \mathcal{z} : 0 \leq i < N}; \nabla \mathcal{z} := \frac{V_{MAX} - V_{MIN}}{N - 1}\]

where \(N \in \mathbb{N}\) and \(V_{MAX}, V_{MIN} \in \mathbb{R}\) are the distribution parameters. The probability of each atom is modeled as

\[Z_\theta(x, a) = \mathcal{z}_i w.p. p_i(x, a) := \frac{\exp{\theta_i(x, a)}}{\sum_j \exp{\theta_j(x, a)}}\]

Action Selection

GenRL uses greedy action selection for categorical DQN wherein the action with the highest Q-values for all discrete regions is selected.

def categorical_greedy_action(agent: DQN, state: torch.Tensor) -> torch.Tensor:
    """Greedy action selection for Categorical DQN

    Args:
        agent (:obj:`DQN`): The agent
        state (:obj:`torch.Tensor`): Current state of the environment

    Returns:
        action (:obj:`torch.Tensor`): Action taken by the agent
    """
    q_value_dist = agent.model(state.unsqueeze(0)).detach()  # .numpy()
    # We need to scale and discretise the Q-value distribution obtained above
    q_value_dist = q_value_dist * torch.linspace(
        agent.v_min, agent.v_max, agent.num_atoms
    )
    # Then we find the action with the highest Q-values for all discrete regions
    # Current shape of the q_value_dist is [1, n_envs, action_dim, num_atoms]
    # So we take the sum of all the individual atom q_values and then take argmax
    # along action dim to get the optimal action. Since batch_size is 1 for this
    # function, we squeeze the first dimension out.
    action = torch.argmax(q_value_dist.sum(-1), axis=-1).squeeze(0)
    return action

Experience Replay

Categorical DQN like other DQNs uses Replay Buffer like other off-policy algorithms. Whenever a transition \((s_t, a_t, r_t, s_{t+1})\) is encountered, it is stored into the replay buffer. Batches of these transitions are sampled while updating the network parameters. This helps in breaking the strong correlation between the updates that would have been present had the transitions been trained and discarded immediately after they are encountered and also helps to avoid the rapid forgetting of the possibly rare transitions that would be useful later on.

    def log(self, timestep: int) -> None:
        """Helper function to log

        Sends useful parameters to the logger.

        Args:
            timestep (int): Current timestep of training
        """
        self.logger.write(
            {
                "timestep": timestep,
                "Episode": self.episodes,
                **self.agent.get_logging_params(),
                "Episode Reward": safe_mean(self.training_rewards),

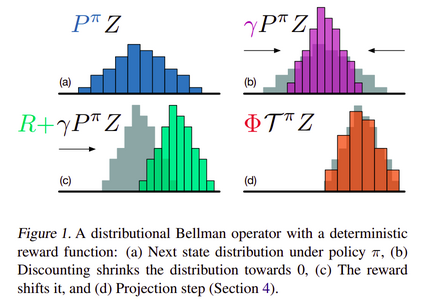
Projected Bellman Update

The sample bellman update \(\hat{\mathcal{T}}Z_\theta\) is projected onto the support of \(Z_\theta\) for the update as shown in the figure below. The bellman update for each atom \(j\) can be calculated as

\[\hat{\mathcal{T}}\mathcal{z_j} := r + \gamma \mathcal{z_j}\]

and then it’s probability \(\mathcal{p_j}(x', \pi{x'})\) is distributed to the neighbours of the update. Here, \((x, a, r, x')\) is a sample transition. The \(i^{th}\) component of the projected update is calculated as

\[(\Phi \hat{\mathcal{T}} Z_\theta(x, a))_i = \sum_{j=0}^{N-1}\left [1 - \frac{\mid \left [\hat{\mathcal{T}}\mathcal{z_j}\right]_{V_{MIN}}^{V_{MAX}} - \mathcal{z_i} \mid}{\Delta \mathcal{z}}\right]_{0}^{1} \mathcal{p_j}(x', \pi(x'))\]

The loss is calculated using KL divergence (cross entropy loss). This is also known as the Bernoulli algorithm

\[D_{KL}(\Phi\hat{\mathcal{T}}Z_\tilde{\theta}(x, a) || Z_\theta (x, a))\]

def categorical_q_target(
    agent: DQN,
    next_states: torch.Tensor,
    rewards: torch.Tensor,
    dones: torch.Tensor,
):
    """Projected Distribution of Q-values

    Helper function for Categorical/Distributional DQN

    Args:
        agent (:obj:`DQN`): The agent
        next_states (:obj:`torch.Tensor`): Next states being encountered by the agent
        rewards (:obj:`torch.Tensor`): Rewards received by the agent
        dones (:obj:`torch.Tensor`): Game over status of each environment

    Returns:
        target_q_values (object): Projected Q-value Distribution or Target Q Values
    """
    delta_z = float(agent.v_max - agent.v_min) / (agent.num_atoms - 1)
    support = torch.linspace(agent.v_min, agent.v_max, agent.num_atoms)

    next_q_value_dist = agent.target_model(next_states) * support
    next_actions = (
        torch.argmax(next_q_value_dist.sum(-1), axis=-1).unsqueeze(-1).unsqueeze(-1)
    )

    next_actions = next_actions.expand(
        agent.batch_size, agent.env.n_envs, 1, agent.num_atoms
    )
    next_q_values = next_q_value_dist.gather(2, next_actions).squeeze(2)

    rewards = rewards.unsqueeze(-1).expand_as(next_q_values)
    dones = dones.unsqueeze(-1).expand_as(next_q_values)

    # Refer to the paper in section 4 for notation
    Tz = rewards + (1 - dones) * 0.99 * support
    Tz = Tz.clamp(min=agent.v_min, max=agent.v_max)
    bz = (Tz - agent.v_min) / delta_z
    l = bz.floor().long()
    u = bz.ceil().long()

    offset = (
        torch.linspace(
            0,
            (agent.batch_size * agent.env.n_envs - 1) * agent.num_atoms,
            agent.batch_size * agent.env.n_envs,
        )
        .long()
        .view(agent.batch_size, agent.env.n_envs, 1)
        .expand(agent.batch_size, agent.env.n_envs, agent.num_atoms)
    )

    target_q_values = torch.zeros(next_q_values.size())
    target_q_values.view(-1).index_add_(
        0,
        (l + offset).view(-1),
        (next_q_values * (u.float() - bz)).view(-1),
    )
    target_q_values.view(-1).index_add_(
        0,
        (u + offset).view(-1),
        (next_q_values * (bz - l.float())).view(-1),
    )
    return target_q_values

Training through the API

from genrl.agents import CategoricalDQN
from genrl.environments import VectorEnv
from genrl.trainers import OffPolicyTrainer

env = VectorEnv("CartPole-v0")
agent = CategoricalDQN("mlp", env)
trainer = OffPolicyTrainer(agent, env, max_timesteps=20000)
trainer.train()
trainer.evaluate()